Jakub Vrána - Lingvistika 1
(Statistické metody zpracování přirozeného jazyka - 12. 12. 2001)
Assign 1: Exploring Entropy and Language Modeling
1.1 The Shannon Game
Used book: burroughs_lostCont.tok
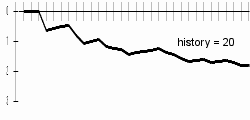
Due to malfunction of computer playing, this game was more irritating than funny. I'm not native English speaker and I didn't read the book, so I had problems with guessing letters - especially those on the beginnings of words. I was usually quite successful in guessing letters inside of the words, but at the beginning of word I sometimes tried about 20 - 25 (!) letters before success. I had this problem even with history length of 20.
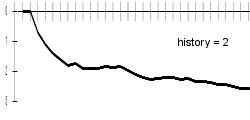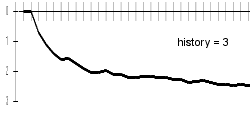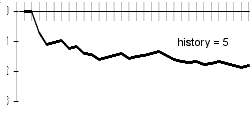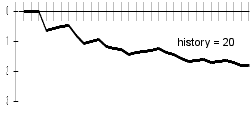
My results are better a bit with longer history lengths; bigger difference can be examined especially in the progresses of charts. With longer histories, charts are sharper - this can be explained by difficult beginning-of-word guessing. Differences are best visible on included animated chart.
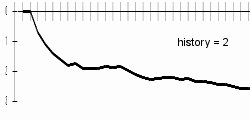 | 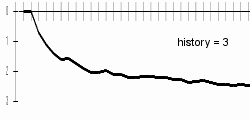 | |
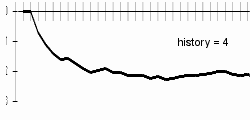 | 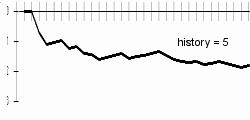 | |
 |  |
Final results
| History length | Entropy |
| 2 | 2.6 |
| 3 | 2.5 |
| 4 | 2.1 |
| 5 | 1.8 |
| 20 | 1.8 |
At the history length of 20, the computer will probably guess letters badly due to data-sparsenes problem.
1.2 Entropy of a Text
Basic statistics and comparison of English and Czech files
| Filename | TEXTEN1 | TEXTCZ1 |
| Number of words in file | 221098 | 222412 |
| Number of characters in file (without \n) | 972917 | 1030631 |
| Average length of word | 4.40 | 4.63 |
| Number of unique words | 9607 | 42826 |
| Number of unique characters | 74 | 117 |
| Total frequency of 10 most frequent words | 29.76% | 23.17% |
| Number of words with frequency equal to 1 | 3811 | 26315 |
| Conditional entropy H(J|I) | 5.28745 | 4.74784 |
| Perplexity PX(J|I) | 39.055 | 26.869 |
In both files, there is the similar number of words and also the similar count of characters, so the average length of word is about 4.5 characters in both files.
The biggest difference is in the number of unique words and also in the number of unique characters. This is of course due to Czech diacritics and high inflection of the Czech language. Higher number of unique words in Czech is reason for much higher number of words with frequency equal to 1 (about one half in Czech against about one third in English). In my opinion, this is also reason for higher frequency of ten most frequent words in English.
Statistics of experiments

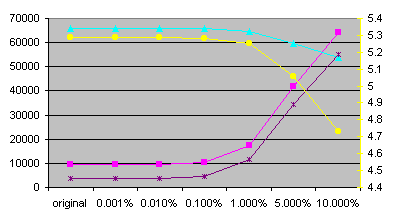
| TEXTEN1 characters | original | 0.001% | 0.010% | 0.100% | 1.000% | 5.000% | 10.000% |
| Number of unique words | 9607 | 9612 | 9709 | 10493 | 17560 | 41967 | 64300 |
| Number of unique characters: | 74 | 74 | 74 | 74 | 74 | 74 | 74 |
| Frequency of 10 most frequent words | 65799 | 65799 | 65777 | 65666 | 64516 | 59674 | 53793 |
| Number of words with frequency equal to 1 | 3811 | 3816 | 3913 | 4701 | 11433 | 34209 | 55151 |
| Average frequency of word | 23.01 | 23.00 | 22.77 | 21.07 | 12.59 | 5.27 | 3.44 |
| Conditional entropy H(J|I): avg | 5.28745 | 5.28742 | 5.28710 | 5.28393 | 5.25100 | 5.05642 | 4.73124 |
| Conditional entropy H(J|I): min | 5.28734 | 5.28697 | 5.28290 | 5.24954 | 5.05196 | 4.72791 | |
| Conditional entropy H(J|I): max | 5.28747 | 5.28729 | 5.28483 | 5.25235 | 5.06092 | 4.73737 | |
| Perplexity PX(J|I): avg | 39.055 | 39.055 | 39.046 | 38.960 | 38.081 | 33.276 | 26.561 |
| Perplexity PX(J|I): min | 39.052 | 39.042 | 38.932 | 38.043 | 33.174 | 26.500 | |
| Perplexity PX(J|I): max | 39.056 | 39.051 | 38.985 | 38.117 | 33.380 | 26.674 |
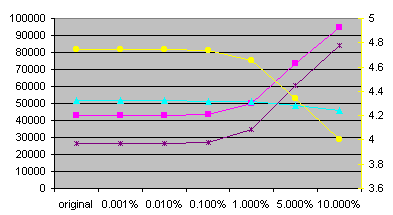
| TEXTCZ1 characters | original | 0.001% | 0.010% | 0.100% | 1.000% | 5.000% | 10.000% |
| Number of unique words | 42826 | 42833 | 42907 | 43581 | 50087 | 73600 | 94438 |
| Number of unique characters: | 117 | 117 | 117 | 117 | 117 | 117 | 117 |
| Frequency of 10 most frequent words | 51533 | 51533 | 51511 | 51466 | 50999 | 48842 | 46173 |
| Number of words with frequency equal to 1 | 26315 | 26322 | 26403 | 27158 | 34434 | 60769 | 84080 |
| Average frequency of word | 5.19 | 5.19 | 5.18 | 5.10 | 4.44 | 3.02 | 2.36 |
| Conditional entropy H(J|I): avg | 4.74784 | 4.74775 | 4.74682 | 4.73853 | 4.65816 | 4.33877 | 4.00646 |
| Conditional entropy H(J|I): min | 4.74769 | 4.74645 | 4.73759 | 4.65615 | 4.33546 | 3.99927 | |
| Conditional entropy H(J|I): max | 4.74779 | 4.74709 | 4.73970 | 4.66073 | 4.34409 | 4.01098 | |
| Perplexity PX(J|I): avg | 26.869 | 26.867 | 26.849 | 26.696 | 25.249 | 20.235 | 16.072 |
| Perplexity PX(J|I): min | 26.866 | 26.843 | 26.678 | 25.214 | 20.189 | 15.992 | |
| Perplexity PX(J|I): max | 26.868 | 26.855 | 26.717 | 25.294 | 20.310 | 16.122 |
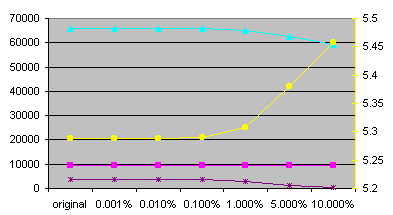
| TEXTEN1 words | original | 0.001% | 0.010% | 0.100% | 1.000% | 5.000% | 10.000% |
| Number of unique words | 9607 | 9607 | 9607 | 9602 | 9574 | 9524 | 9566 |
| Number of unique characters: | 74 | 74 | 74 | 74 | 74 | 74 | 74 |
| Frequency of 10 most frequent words | 65799 | 65799 | 65799 | 65732 | 65158 | 62460 | 59321 |
| Number of words with frequency equal to 1 | 3811 | 3811 | 3804 | 3717 | 3029 | 1198 | 456 |
| Average frequency of word | 23.01 | 23.01 | 23.01 | 23.03 | 23.09 | 23.21 | 23.11 |
| Conditional entropy H(J|I): avg | 5.28745 | 5.28747 | 5.28764 | 5.28948 | 5.30705 | 5.37983 | 5.45848 |
| Conditional entropy H(J|I): min | 5.28742 | 5.28749 | 5.28926 | 5.30560 | 5.37661 | 5.45529 | |
| Conditional entropy H(J|I): max | 5.28752 | 5.28777 | 5.29005 | 5.30878 | 5.38540 | 5.46334 | |
| Perplexity PX(J|I): avg | 39.055 | 39.056 | 39.061 | 39.110 | 39.590 | 41.638 | 43.971 |
| Perplexity PX(J|I): min | 39.055 | 39.057 | 39.104 | 39.550 | 41.545 | 43.874 | |
| Perplexity PX(J|I): max | 39.057 | 39.064 | 39.126 | 39.637 | 41.799 | 44.119 |
| TEXTCZ1 words | original | 0.001% | 0.010% | 0.100% | 1.000% | 5.000% | 10.000% |
| Number of unique words | 42826 | 42826 | 42825 | 42802 | 42549 | 41815 | 41282 |
| Number of unique characters: | 117 | 117 | 117 | 117 | 117 | 117 | 117 |
| Frequency of 10 most frequent words | 51533 | 51533 | 51511 | 51466 | 51021 | 48953 | 46395 |
| Number of words with frequency equal to 1 | 26315 | 26314 | 26304 | 26179 | 24874 | 20029 | 15869 |
| Average frequency of word | 5.19 | 5.19 | 5.19 | 5.20 | 5.23 | 5.32 | 5.39 |
| Conditional entropy H(J|I): avg | 4.74784 | 4.74784 | 4.74779 | 4.74701 | 4.73905 | 4.69926 | 4.63712 |
| Conditional entropy H(J|I): min | 4.74780 | 4.74771 | 4.74670 | 4.73828 | 4.69761 | 4.63184 | |
| Conditional entropy H(J|I): max | 4.74786 | 4.74791 | 4.74770 | 4.74089 | 4.70157 | 4.64195 | |
| Perplexity PX(J|I): avg | 26.869 | 26.868 | 26.867 | 26.853 | 26.705 | 25.979 | 24.884 |
| Perplexity PX(J|I): min | 26.868 | 26.866 | 26.847 | 26.691 | 25.949 | 24.793 | |
| Perplexity PX(J|I): max | 26.869 | 26.870 | 26.866 | 26.739 | 26.020 | 24.967 |
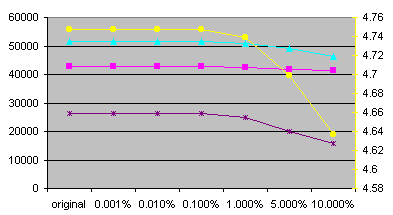
We can see that differences between minimal and maximal entropies are very small for each experiment. The reason is that I used good pseudo-random number generator (Mersenne Twister). Also, the number of random values used for getting entropies is very high. So I will talk just about average values from now. Statistics for mess-ups are get from random experiment (the tenth one).
The number of unique characters is the same for all mess-ups. Practical, it could change (decrease) only if there was a single word with some unique character and this word was chosen to be replaced and not to replace another word. Other possibilities are almost impossible and as we can see, described possibility is also almost impossible.
The number of words in file can't change by messing up. Also the number of characters in file can't change by character messing up and I predicted that also it doesn't change much for word messing up. So I didn't watch these values.
Some more interesting facts
The number of unique words rapidly raises with character messing-up. For 10% messing-up factor, the number of unique words raises more than twice for Czech and more than six times for English. So the rate of number of unique words between English and Czech moves from about one quarter to about two thirds. The number of unique words lowers a bit with word messing-up.
The number of words with frequency equal-to-one lowers for word messing-up and raises for character messing-up. For 10% character messing-up factor, it raises three times for Czech and fourteen times for English. For 10% word messing-up factor, it lowers 1.6 times for Czech and eight times for English. In my opinion, the number of words with frequency equal-to-one lowers more in English due to the smaller absolute number of unique words. Similar reason can be used for disproportion in raising the number of words with frequency equal-to-one in character messing-up.
Final result of the experiments - entropy and perplexity
Generally, entropy is lower in Czech due to higher number of unique words and due to higher number of words with frequency equal-to-one (call them isolated words). We can sum it up that the average frequency of words is lower in Czech than in English. So it is easier to predict words from one-word context because there is only one possibility after isolated words. Generally, it is easier to predict words after words with low frequency. This fact is reason for lowering the entropy when messing-up characters.
The trend of entropy during word messing-up is strange at a glance. It raises for English but lowers for Czech. I think that this can be explained like that: In English, the number of unique words remains almost the same (due to the small absolute number of these words). In opposite, the number of isolated words lowers. So it is harder to predict next word. In Czech, the number of unique words lowers. So it is easier to predict next word, because there are fewer choices. But - in my opinion, decreasing the number of unique words (by 4%) shouldn't be so important as decreasing the number of isolated words (by 40%). So I can't explain lowering the entropy in the Czech text sufficiently.
Behavior of perplexity is the same as entropy (better visible due to the exponential type of this function). Perplexity equal to 27 just says something like that we need about 27 attempts to guess next word from one-word context.
Paper and pencil exercise
By appending text with conditional entropy E to the end of another text with the same conditional entropy, the conditional entropy of this new text remains almost the same in case that these two texts don't share any vocabulary items. We can take it in like that: It is equally hard to predict the next word from one-word context because texts don't share any vocabulary items.
Mathematical prove: P(j|i) remains the same (due to different vocabularies), so the log part of the sum remains also the same. P(i,j) lowers to P(i,j) * |T1| / (|T1| + |T2|) for words from first text, so sum of words from first text lowers to E1 * |T1| / (|T1| + |T2|). Similarly the sum for words from second text lowers to E2 * |T2| / (|T1| + |T2|). Since the original entropies are equal, the final sum is E * (|T1| + |T2|) / (|T1| + |T2|) = E.
I wrote that entropy remains almost the same. This relates to the boundary of the texts. If the last word from first text is unique in this text, the final entropy lowers a bit (or remains the same if we included the start-of-text symbol) otherwise it raises a bit.
1.3 Cross-Entropy and Language Modeling
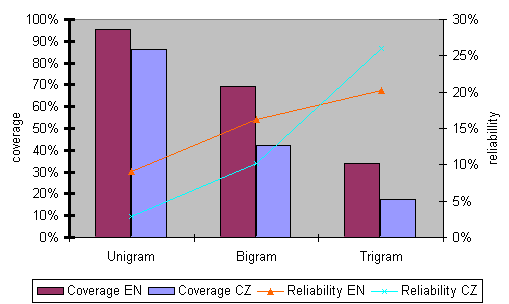
| Coverage | English | Czech |
| Unigram | 96% | 86% |
| Bigram | 69% | 42% |
| Trigram | 34% | 18% |
The coverage of n-gram is defined as the number of n-grams from the test data seen in the training data divided by the size of the test data.
Generally, the coverage is higher in English all for unigrams, bigrams and trigrams. So the cross entropy will be probably higher in Czech regardless of other facts.
| Reliability | English | Czech |
| Unigram | 9.0% | 2.8% |
| Bigram | 16.3% | 10.2% |
| Trigram | 20.2% | 26.0% |
The reliability of n-gram is defined as the average of the conditional probabilities of n-grams with seen context. So, for all words J with context I in the test data, do the following: If we have seen context I of word J in the training data, add P(J|I) to the average.
Unigram reliability is much higher in English due to significantly higher average frequency of word than in Czech. In opposite, trigram reliability is higher in Czech due mainly to the inflection (e.g. if adjective is in accusative, the following noun should be also in accusative).
| Weights and cross entropy | English | Czech |
| lambda0 (uniform weight) | 0.07 | 0.14 |
| lambda1 (unigram weight) | 0.25 | 0.43 |
| lambda2 (bigram weight) | 0.49 | 0.25 |
| lambda3 (trigram weight) | 0.19 | 0.19 |
| Cross entropy | 7.47 | 10.22 |
Bigram weight is higher in English. To compensate it, unigram and uniform weights are higher in Czech. These are higher also due to the small coverage of bigrams and trigrams in Czech. Trigram weight is the same for English and for Czech because lower trigram coverage in Czech is compensated by its higher reliability (and also because it is used uniform probability for unseen contexts). Cross entropy is lower in English, so it is easier to predict English on this size of data.
I used the EM Algorithm to count the weight parameters. For unseen context, this algorithm uses uniform probability. I thought about this algorithm for long time - about the correctness, accuracy and about the relation of weights with coverage and reliability. I think that weights are deformed a bit due to usage of uniform probabilities for unseen contexts. I tried to use zero probability for unseen contexts (regardless of it doesn't sum to 1) and the trigram weight was 0.14 for English and 0.06 for Czech. I also improved EM algorithm by usage of (n-1)-gram for unseen contexts instead of uniform probability. There are the results:
| (n-1)-gram for unseen contexts | English | Czech |
| lambda0 (uniform weight) | 0.10 | 0.26 |
| lambda1 (unigram weight) | 0.23 | 0.37 |
| lambda2 (bigram weight) | 0.45 | 0.20 |
| lambda3 (trigram weight) | 0.22 | 0.17 |
| Cross entropy | 7.42 | 10.21 |
Uniform weights are higher than in previous case because it was "distributed" to the other weights over there. I was surprised that the bigram weight is smaller than trigram weight at a glance: For unseen context in trigram, it does use the bigram probability. And trigrams are more reliable than bigrams, so trigram weight should be greater than bigram weight. The reason is that reliability of bigrams used concurrent to trigrams is higher - 28.7% for both English and Czech.
Cross entropy is lower a bit by usage of this algorithm. Anyway, I used the original EM algorithm for tweaks to provide comparable data.
Tweaks
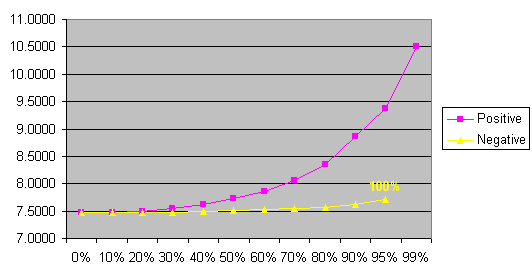
| TEXTEN1 | lambda0 | lambda1 | lambda2 | lambda3 | Entropy |
| 0% | 0.0699 | 0.2527 | 0.4851 | 0.1923 | 7.4669 |
| 10% | 0.0629 | 0.2274 | 0.4366 | 0.2731 | 7.4712 |
| 20% | 0.0559 | 0.2022 | 0.3880 | 0.3538 | 7.4998 |
| 30% | 0.0489 | 0.1769 | 0.3395 | 0.4346 | 7.5508 |
| 40% | 0.0420 | 0.1516 | 0.2910 | 0.5154 | 7.6254 |
| 50% | 0.0350 | 0.1264 | 0.2425 | 0.5962 | 7.7280 |
| 60% | 0.0280 | 0.1011 | 0.1940 | 0.6769 | 7.8672 |
| 70% | 0.0210 | 0.0758 | 0.1455 | 0.7577 | 8.0608 |
| 80% | 0.0140 | 0.0505 | 0.0970 | 0.8385 | 8.3488 |
| 90% | 0.0070 | 0.0253 | 0.0485 | 0.9192 | 8.8582 |
| 95% | 0.0035 | 0.0126 | 0.0243 | 0.9596 | 9.3695 |
| 99% | 0.0007 | 0.0025 | 0.0049 | 0.9919 | 10.5080 |
| -10% | 0.0716 | 0.2587 | 0.4966 | 0.1731 | 7.4701 |
| -20% | 0.0733 | 0.2647 | 0.5082 | 0.1538 | 7.4753 |
| -30% | 0.0749 | 0.2708 | 0.5197 | 0.1346 | 7.4827 |
| -40% | 0.0766 | 0.2768 | 0.5313 | 0.1154 | 7.4927 |
| -50% | 0.0782 | 0.2828 | 0.5428 | 0.0962 | 7.5057 |
| -60% | 0.0799 | 0.2888 | 0.5544 | 0.0769 | 7.5225 |
| -70% | 0.0816 | 0.2948 | 0.5659 | 0.0577 | 7.5443 |
| -80% | 0.0832 | 0.3008 | 0.5775 | 0.0385 | 7.5733 |
| -90% | 0.0849 | 0.3069 | 0.5890 | 0.0192 | 7.6148 |
| -100% | 0.0866 | 0.3129 | 0.6006 | 0.0000 | 7.7042 |
| TEXTCZ1 | lambda0 | lambda1 | lambda2 | lambda3 | Entropy |
| 0% | 0.1354 | 0.4283 | 0.2459 | 0.1903 | 10.2198 |
| 10% | 0.1219 | 0.3855 | 0.2213 | 0.2713 | 10.2253 |
| 20% | 0.1083 | 0.3427 | 0.1967 | 0.3523 | 10.2554 |
| 30% | 0.0948 | 0.2998 | 0.1721 | 0.4332 | 10.3079 |
| 40% | 0.0812 | 0.2570 | 0.1475 | 0.5142 | 10.3841 |
| 50% | 0.0677 | 0.2142 | 0.1230 | 0.5952 | 10.4879 |
| 60% | 0.0542 | 0.1713 | 0.0984 | 0.6761 | 10.6279 |
| 70% | 0.0406 | 0.1285 | 0.0738 | 0.7571 | 10.8210 |
| 80% | 0.0271 | 0.0857 | 0.0492 | 0.8381 | 11.1059 |
| 90% | 0.0135 | 0.0428 | 0.0246 | 0.9190 | 11.6035 |
| 95% | 0.0068 | 0.0214 | 0.0123 | 0.9595 | 12.0958 |
| 99% | 0.0014 | 0.0043 | 0.0025 | 0.9919 | 13.1681 |
| -10% | 0.1386 | 0.4384 | 0.2517 | 0.1713 | 10.2227 |
| -20% | 0.1418 | 0.4485 | 0.2575 | 0.1523 | 10.2276 |
| -30% | 0.1450 | 0.4586 | 0.2632 | 0.1332 | 10.2347 |
| -40% | 0.1481 | 0.4686 | 0.2690 | 0.1142 | 10.2444 |
| -50% | 0.1513 | 0.4787 | 0.2748 | 0.0952 | 10.2571 |
| -60% | 0.1545 | 0.4888 | 0.2806 | 0.0761 | 10.2736 |
| -70% | 0.1577 | 0.4988 | 0.2864 | 0.0571 | 10.2953 |
| -80% | 0.1609 | 0.5089 | 0.2922 | 0.0381 | 10.3247 |
| -90% | 0.1641 | 0.5190 | 0.2979 | 0.0190 | 10.3681 |
| -100% | 0.1672 | 0.5290 | 0.3037 | 0.0000 | 10.4897 |
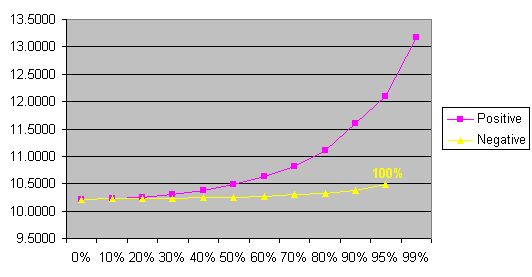
Cross entropy raises both for increasing the trigram weight and also for decreasing it. This could be expected because computed weights are supposed to be the best. Cross entropy raises much more by increasing the trigram weight than by decreasing it. It says that it is better to use the trigram weights less (or not at all) than depends only on them. And, of course, the absolute value of the weight is less then one half, so increasing e.g. 0.2 to 0.6 (by tweak factor +50%) is more visible than decreasing it to 0.1 (by tweak factor -50%).
By decreasing the trigram weight, cross entropy raises only a little. This could be explained that on this (small) data the trigrams are not so important, nearly all information is hidden in bigrams.
Held-out data
If we count lambda values on training data, we should get 100% for trigram weight and 0% for the others. I tested the correctness of my program by running on training data with knowledge of this fact. If we try to count weights on testing data, it will be similar as on held-out data. But we would not be allowed to use these data for testing because weights will be adjusted to this data. But, in my opinion, we can add the held-out data to the training data after computation of weights.
Source codes